算法与数据结构(二) - 数组
定义
数组(Array)是有序的元素序列。 [1] 若将有限个类型相同的变量的集合命名,那么这个名称为数组名。组成数组的各个变量称为数组的分量,也称为数组的元素,有时也称为下标变量。用于区分数组的各个元素的数字编号称为下标。数组是在程序设计中,为了处理方便, 把具有相同类型的若干元素按有序的形式组织起来的一种形式。 [1] 这些有序排列的同类数据元素的集合称为数组。
数组常见问题算法
二分查找
二分查询法就是讲数据进行两份化处理. 左边区域left 右边区域right.再取中间值,进行比较,判断要求数据在哪个区域
大家写二分法经常写乱,主要是因为对区间的定义没有想清楚,区间的定义就是不变量。要在二分查找的过程中,保持不变量,就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作,这就是循环不变量规则。
写二分法,区间的定义一般为两种,左闭右闭即[left, right],或者左闭右开即[left, right)。
例题:给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4 示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1 提示:
- 你可以假设 nums 中的所有元素是不重复的。
- n 将在 [1, 10000]之间。
- nums 的每个元素都将在 [-9999, 9999]之间。
假设存在数组:1,2,3,4,7,9,10中查找元素2.
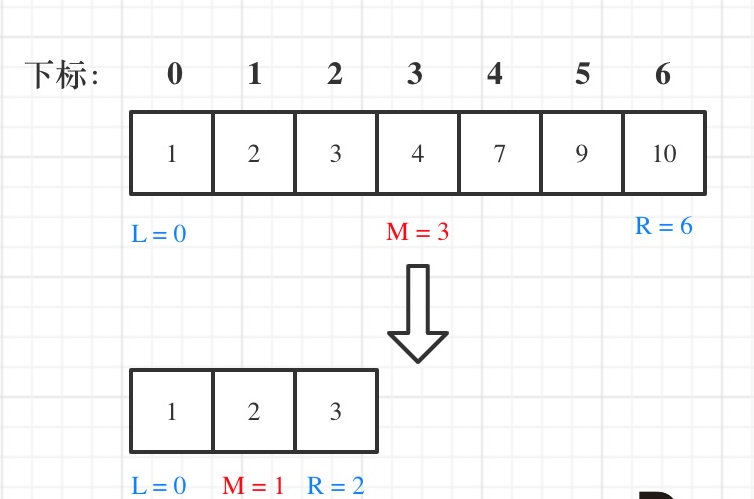
public static int twolinkSearch(int[] nums, int target) {
//当 target 小于nums[0] 或者nums[nums.length - 1]时返回-1
if (target < nums[0] || target > nums[nums.length - 1]) {
return -1;
}
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + ((right - left) / 2); // 防止溢出 等同于(left + right)/2
if (nums[mid] ==target)
return mid;
else if (nums[mid] < target) // 中间数小于目标值,则目标值在右半区
left=mid+1;
else if (nums[mid]>target) // 中间数大于目标值,则目标值在左半区
return right=mid-1;
}
return -1;
}移除元素
要知道数组的元素在内存地址中是连续的,不能单独删除数组中的某个元素,只能覆盖。
例题:给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
提示:不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并原地修改输入数组。
示例 1:
给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。 你不需要考虑数组中超出新长度后面的元素。
示例 2:
给定 nums = [0,1,2,2,3,0,4,2], val = 2, 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。
暴力循环解法

使用两层for循环,一个for循环遍历数组元素 ,第二个for循环更新数组。
// 时间复杂度:O(n^2)
// 空间复杂度:O(1)
public static int foreachDeleteVar(int[] nums,int target){
int length = nums.length;
for (int i=0;i<length;i++){
if (nums[i]==target){ // 发现需要移除的元素,就将后面数组集体向前移动一位,进行覆盖操作
for (int j=i+1;j<length;j++){
nums[j-1]=nums[j];
}
i--; // 因为下表i以后的数值都向前移动了一位,所以i也向前移动一位
length--; // 此时数组的大小-1
}
}
return length;
}双指针法
双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
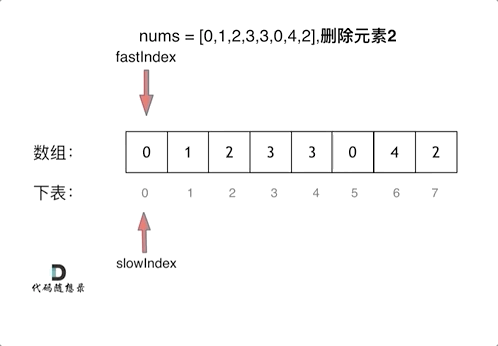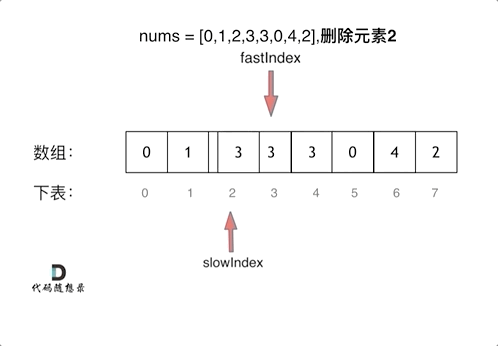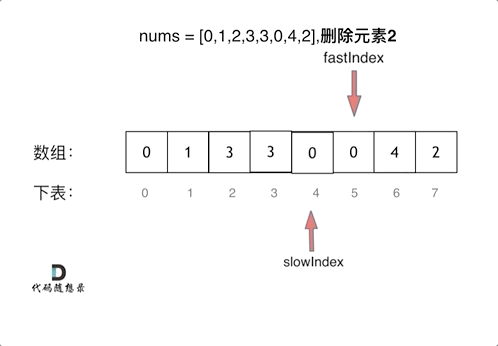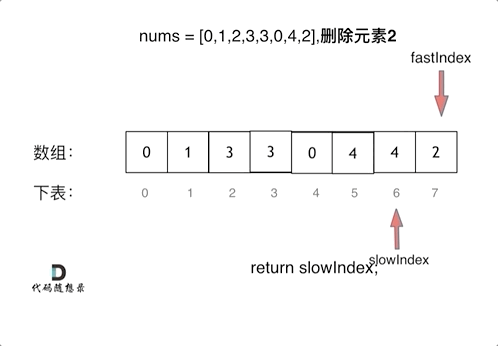
双指针法(快慢指针法)在数组和链表的操作中是非常常见的,很多考察数组、链表、字符串等操作的面试题,都使用双指针法。
// 时间复杂度:O(n)
// 空间复杂度:O(1)
public static int fastSlowIndexDeleteVar(int[] nums, int target) {
int fast = 0;
int slow;
for (slow = 0; fast < nums.length; fast++) {
if (nums[fast] != target) {
nums[slow] = nums[fast];
slow++;
}
}
return slow;
}滑动窗口法
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。通常使用在求和的数组上.
滑动窗口也可以理解为双指针法的一种!只不过这种解法更像是一个窗口的移动,所以叫做滑动窗口更适合一些。
例题:给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例:
输入:s = 7, nums = [2,3,1,2,4,3] 输出:2 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
使用滑动窗口法:
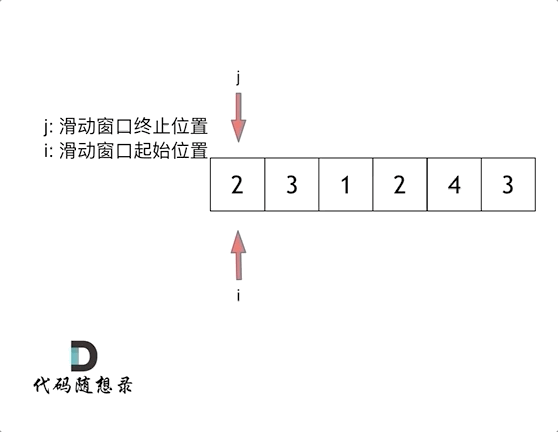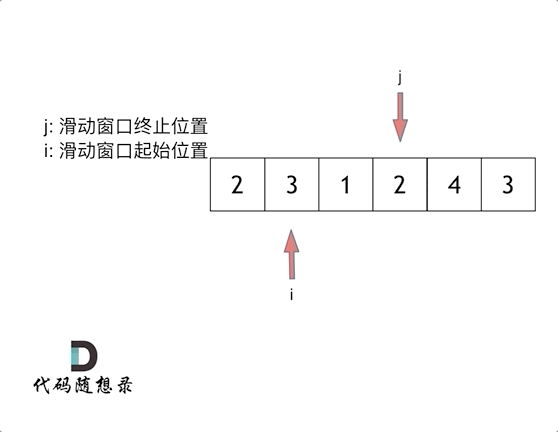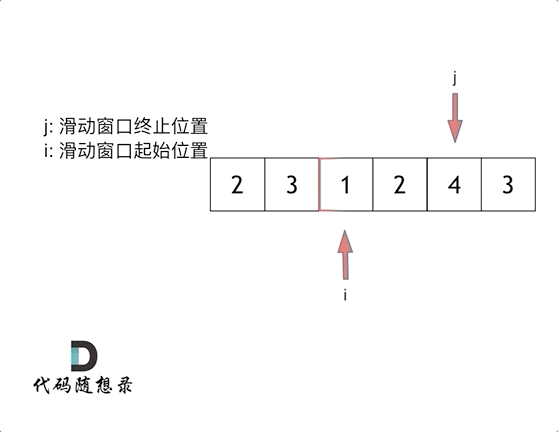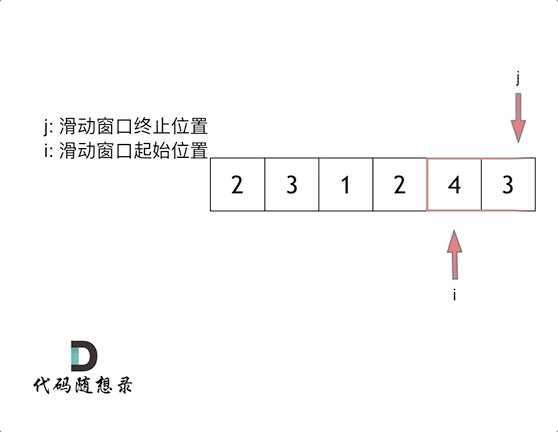
本题中实现滑动窗口,主要确定如下三点:
- 窗口内是什么?
- 如何移动窗口的起始位置?
- 如何移动窗口的结束位置?
窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。
窗口的起始位置如何移动:如果当前窗口的值大于s了,窗口就要向前移动了(也就是该缩小了)。
窗口的结束位置如何移动:窗口的结束位置就是遍历数组的指针,窗口的起始位置设置为数组的起始位置就可以了。
public static int miniSubLen(int[] nums, int target) {
int start = 0;
int sum = 0;
int result = Integer.MAX_VALUE;
for (int end = 0;end < nums.length;end++){
sum += nums[end];
while (sum >= target){ //判断结果是否大于或等于目标值
result = Math.min(result,end - start + 1); //判断结果的数组长度,如果更小则替代原结果
sum -= nums[start++]; //减掉开始指针的值,并将开始指针向前移动
}
}
return result == Integer.MAX_VALUE ? 0 : result;
}数列排序
进行数列排序算法:
插入排序
每次将一个数字插入一个有序的数组里,成为一个长度更长的有序数组,有限次操作以后,数组整体有序。
/**
* 时间复杂度:O(N^2)
* 空间复杂度:O(1)
*/
public int[] sortArray(int[] nums) {
int len = nums.length;
// 循环不变量:将 nums[i] 插入到区间 [0, i) 使之成为有序数组
for (int i = 1; i < len; i++) {
int temp = nums[i]; // 提前将其当前指针的值存储
int j = i; //用作遍历当前指针前的元素的指针
//判断前一个数是否大于当前数, 注意边界 j > 0
while (j > 0 && nums[j - 1] > temp) {
nums[j] = nums[j - 1];
j--;
}
nums[j] = temp;
}
return nums;
}在小区间内执行排序任务的时候,可以转向使用「插入排序」。
归并排序
归并这个词语的含义就是合并,并入的意思.
归并排序使用的就是分治思想。顾名思义就是分而治之,将一个大问题分解成若干个小的子问题来解决。
将原数组分区域,分别排序,借助额外空间,合并分区域的有序数组,得到更长的有序数组.
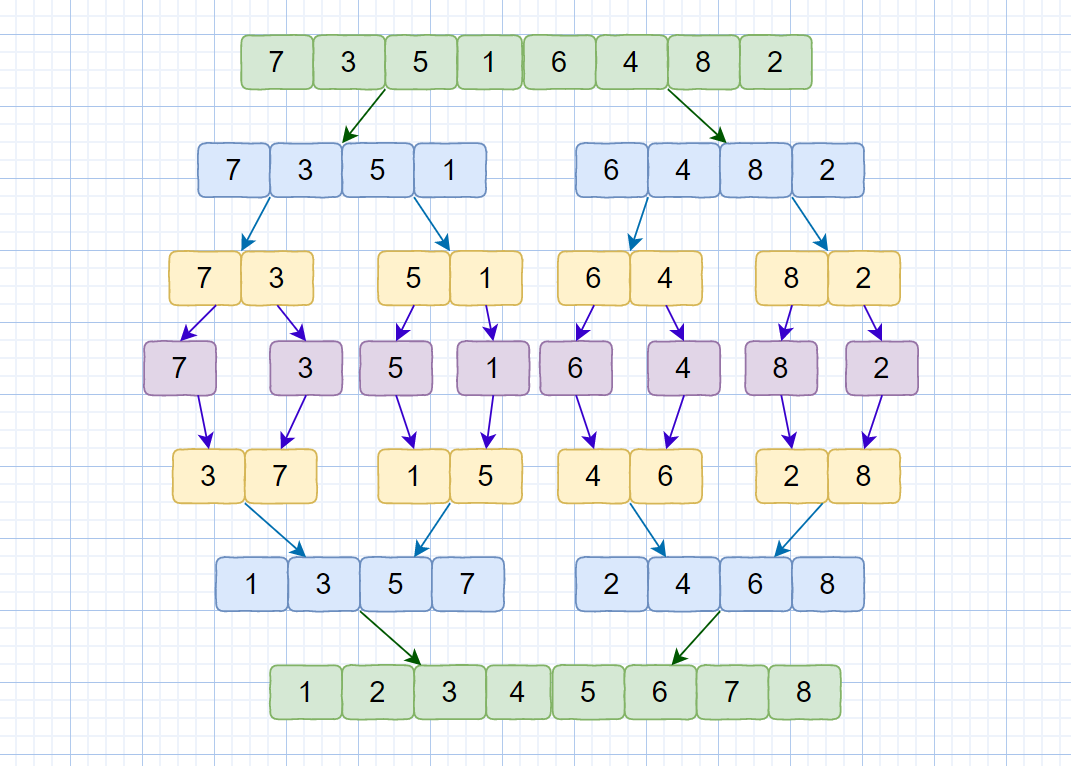
而其中的归并主要实现思想为:
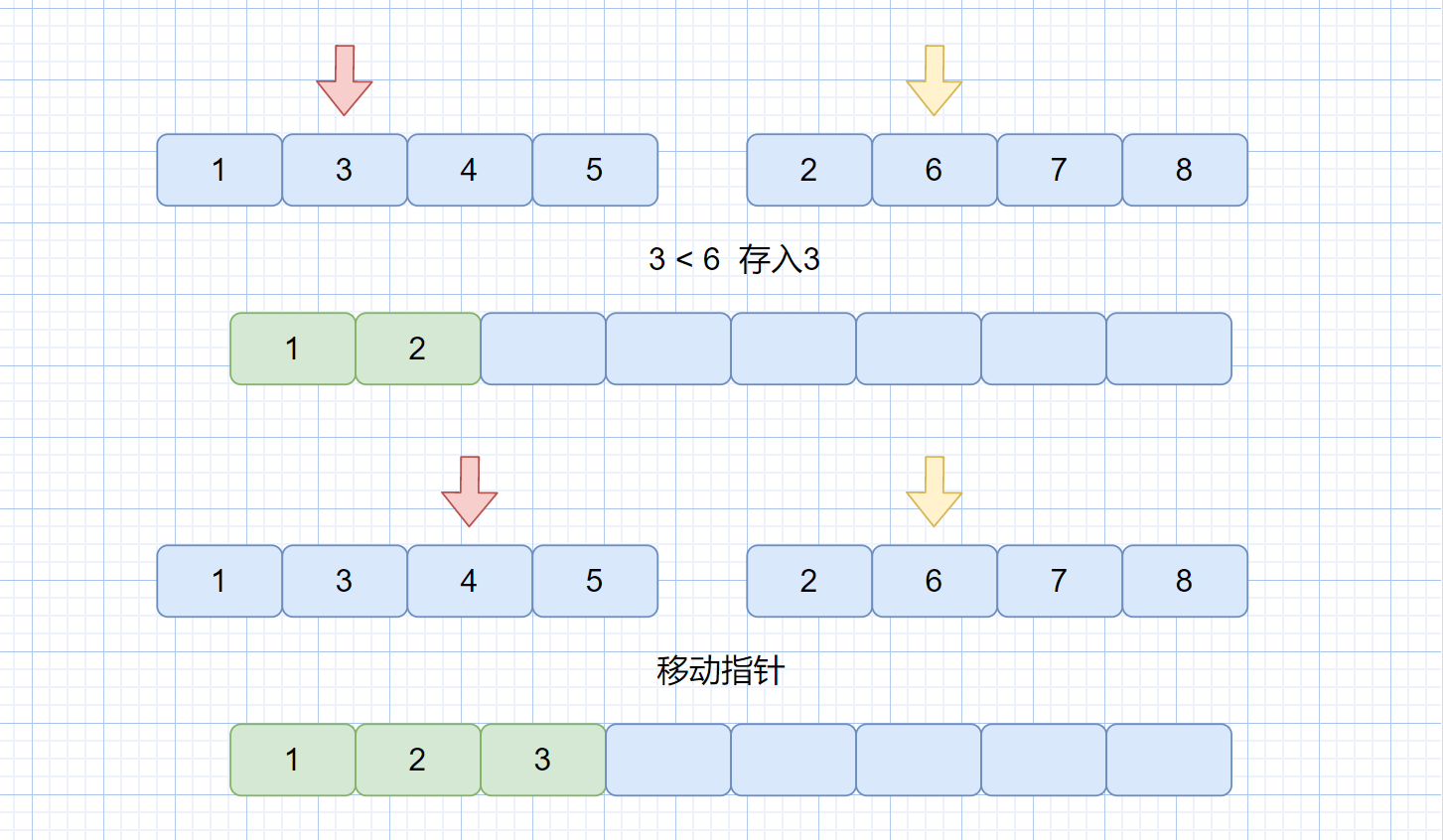
通过双指针从左自右比较两个指针指向的值,将较小的一方存入大集合中,存入之后较小一方的指针向前移动,并继续比较,直到某一小集合的元素全部都存到大集合中。
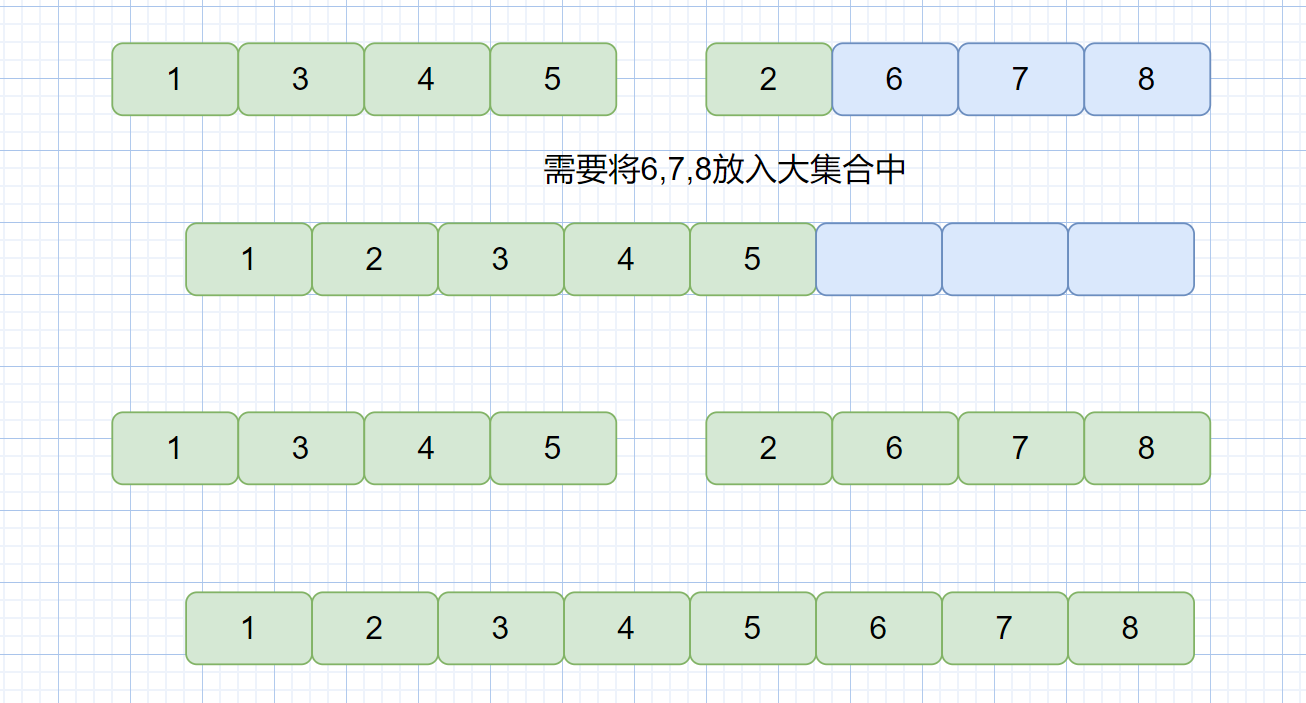
当某一小集合元素全部放入大集合中(指针到尾部无法继续后),则需将另一小集合中剩余的所有元素存到大集合中.
public static void sortIntArray(int[] target) {
mergeSort(target, 0, target.length - 1);
}
/**
* 对数组 nums 的子区间 [left, right] 进行归并排序
*
*/
private static void mergeSort(int[] nums, int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
mergeSort(nums, left, mid);
mergeSort(nums, mid + 1, right);
//合并小区域数组排序
mergeOfTwoSortedArray(nums, left, mid, right);
}
}
/**
* 合并两个有序数组:先把值复制到临时数组,再合并回去
*
*/
private static void mergeOfTwoSortedArray(int[] arr, int left, int mid, int right) {
/** 第一步,定义一个新的临时数组 **/
int[] tempArr = new int[right - left + 1];
// 两个数列的指针
int temp1 = left, temp2 = mid + 1;
int index = 0;
/** 第二步,比较每个指针指向的值,小的存入大集合 **/
while (temp1 <= mid && temp2 <= right) {
if (arr[temp1] <= arr[temp2]) {
tempArr[index] = arr[temp1];
index++;
temp1++;
} else {
tempArr[index] = arr[temp2];
index++;
temp2++;
}
}
/** 第三步,将未全部存入的小集合剩余元素存到大集合中 **/
if (temp1 <= mid) {
System.arraycopy(arr, temp1, tempArr, index, mid - temp1 + 1);
}
if (temp2 <= right) {
System.arraycopy(arr, temp2, tempArr, index, right - temp2 + 1);
}
System.arraycopy(tempArr,0,arr,0+left,right-left+1);
}while 中两个指针循环,可以在内部进行判断,当其指针到边缘位置时break退出,避免不必要的循环步骤,性能又能提升40%。
while (nums[less]<pivot){
if (less==right){
break;
}
less++;
}
while (nums[greater]>pivot){
if (greater==left){
break;
}
greater--;
}| 算法名称 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | 空间复杂度 | 是否稳定 |
|---|---|---|---|---|---|
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 |
快速排序
快速排序也是一种分治的排序算法.它将数组通过切分(partition)分成两个子数组,将两部分独立地排序.快速排序和归并排序是互补的.
快速排序基本思想:
1.先从数组中找一个基准数
2.让其他比它大的元素移动到数列一边,比他小的元素移动到数列另一边,从而把数组拆解成两个部分。
3.再对左右区间重复第二步,直到各区间只有一个数。
在快速排序中,首先随机打乱数组排序.然后取出切分元素,它把数组大于小于它的进行划分.
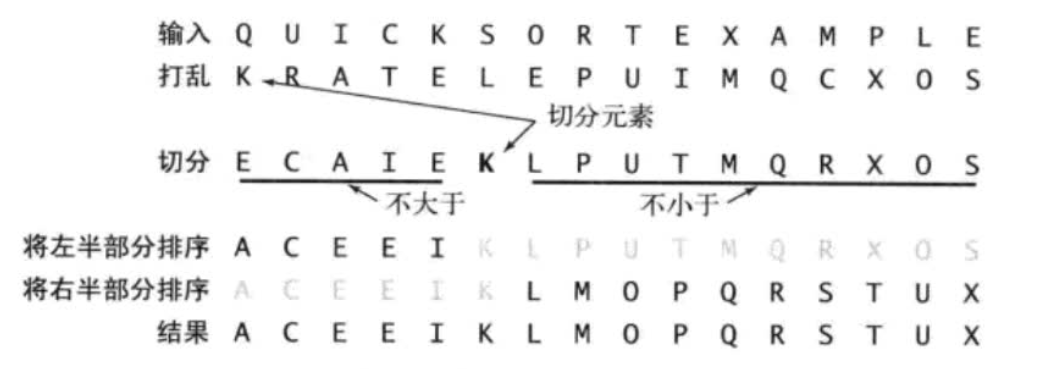
然后分别将左右部分循环进行快速排序,

一边循环到只有大小一为止,排序到最后直接合并即可(不需要像归并排序最后还需要合并排序).
- 版本 1:基本版本:把等于切分元素的所有元素分到了数组的同一侧,但可能会造成递归树倾斜;
/**
* 快速排列
* @param nums
* @param left
* @param right
*/
public void quickSort(int[] nums, int left, int right) {
// 判断是否 长度是否为0 ,为0则为排序完毕的元素
if (right - left + 1 <= 0){
return;
}
//获取切点元素位置
int pIndex = partition(nums, left, right);
quickSort(nums, left, pIndex - 1); //左侧
quickSort(nums, pIndex + 1, right); //右侧
}
/**
* 切分数组
*
* @param nums
* @param left
* @param right
*/
private int partition(int[] nums, int left, int right) {
//获取随机下标数(切分元素)
int randomIndex = new Random().nextInt(right - left + 1) + left;
swap(nums, left, randomIndex); //将头部与切分元素进行交换
// 切分元素值
int pivot = nums[left];
// 切分元素下标位置
int less = left;
for (int i = left + 1; i <= right; i++) {
if (nums[i] < pivot) { //指针的值小于切分值
less++;
swap(nums, i, less); //切分值与其互换位置
}
}
swap(nums, left, less);
return less;
}
/**
* 交换两个值位置
*/
private void swap(int[] nums, int index1, int index2) {
int temp = nums[index1];
nums[index1] = nums[index2];
nums[index2] = temp;
}版本2:双指针法 - 把等于切分元素的所有元素等概率地分到了数组的两侧,避免了递归树倾斜,递归树相对平衡;
/**
* 快速排列
*
* @param nums
* @param left
* @param right
*/
public void quickSort(int[] nums, int left, int right) {
if (left < right) {
int pIndex =partition(nums,left,right);
quickSort(nums,left,pIndex-1);
quickSort(nums,pIndex+1,right);
}
}
public int partition(int[] nums, int left, int right) {
int randomIndex = left + new Random().nextInt(right - left + 1);
swap(nums, randomIndex, left);
int pivot = nums[left];
// 两个指针:一个从前到后,一个从后向前
int less = left + 1;
int greater = right;
while (true){
while (less<=right&&nums[less]<pivot){
less++;
}
while (greater>left&& nums[greater]>pivot){
greater--;
}
// 当小指针大于或等于大指针退出循环
if (less>=greater){
break;
}
// 当less指针大于等于 且greater指针小于等于时,同时双指针移动
swap(nums,less,greater);
less++;
greater--;
}
swap(nums,left,greater);
return greater;
}
public void swap(int[] nums, int index1, int index2) {
int temp = nums[index1];
nums[index1] = nums[index2];
nums[index2] = temp;
}