算法与数据结构(三)-快速排序详解
前言
在算法与数据结构(二) - 数组中我们简绍了快速排序算法,其中快速排序部分描述为《算法四》中的,理解起来有点难度。本篇文章专门用来分析其快速排序的具体过程。
解析步骤
快速排序详细操作分为三步骤:
寻找 基准元素。通常我们使用其快排里,我们只要记住把头部元素当作基准元素就够了(假设数组元素是随机分布的)
使用左右双指针来进行扫描,左边指针向右扫描,右边指针向左扫描。
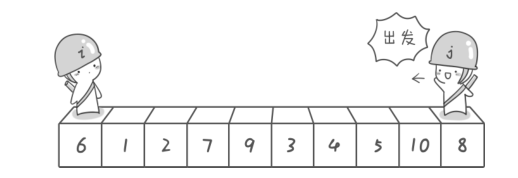
(图源来自《啊哈,算法》)
这里我们选取首位6 来作为基准元素。
这时候,左右游标开始分别向右/左移动,它们遵循的规则分别是:
- 左游标向右扫描, 跨过所有小于基准元素的数组元素, 直到遇到一个大于或等于基准元素的数组元素, 在那个位置停下。
- 右游标向左扫描, 跨过所有大于基准元素的数组元素, 直到遇到一个小于或等于基准元素的数组元素,在那个位置停下。
当左右指针扫描都结束时,两个指针停下的地方如果未相交的话,那么就交换两指针下的元素。
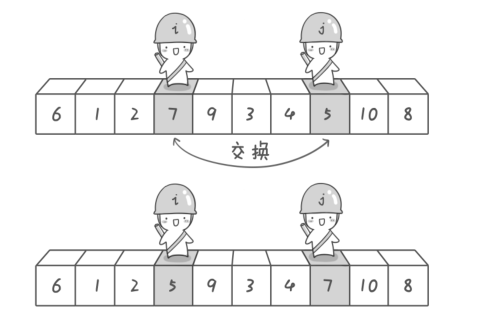
交换之后,会发现两指针又会实现其条件,所以继续执行第二步扫描操作,反复循环。
最终两指针会相交(至于是左指针还是右指针最后移动,这个取决于谁先开始,但和这结果、性能无关),从而停下。
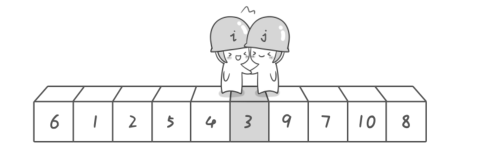
这时,会发现,数组大致 状态是 : 基准元素(中间值)+小于中间值的数组+大于中间值的数组。
所以这时我们需要将其相交的元素与其基准元素 交换,这样就是 小于中间值的数组+基准元素(中间值)+大于中间值的数组。
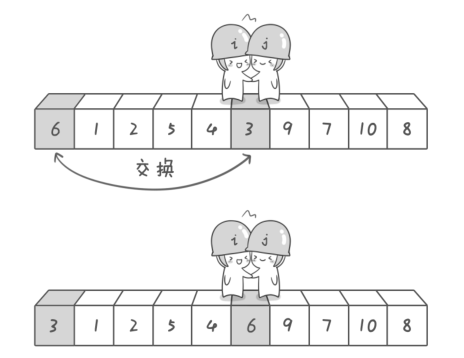
对小于中间值的数组,和大于中间值的数组分别 再次执行 1-4步骤。也就是再循环多次操作对两边数组。使用递归即可。
这样的话小于中间值的数组和大于中间值的数组就会被反复排序正常。
代码实现
下面使用Java代码表示整个过程:
private static void sort(int[] a, int low, int high) {
// 终止递归
if (high <= low) {
return;
}
// 调用partition进行切分
int j = partition(a, low, high);
// 对上一轮排序(切分)时,基准元素左边的子数组进行递归
sort(a, low, j - 1);
// 对上一轮排序(切分)时,基准元素右边的子数组进行递归
sort(a, j + 1, high);
}
/**
* 数组切分
* 将数组按照基准元素分为两部分
* @return 最终基准元素位置
*/
private static int partition(int[] a, int low, int high) {
// i, j为左右扫描指针 PS: 思考下为什么j比i 多加一个1呢?
int i = low, j = high + 1;
// pivotkey 为选取的基准元素(头元素)
int pivotkey = a[low];
while (true) {
// 右游标左移
while (a[--j] > pivotkey) {
if (j == low) {
break;
}
}
// 左游标右移
while (a[++i] < pivotkey) {
if (i == high) {
break;
}
}
// 左右游标相遇时候停止, 所以跳出外部while循环
if (i >= j) {
break;
}
// 左右游标都中途停止时,互相交换元素
exchange(a, i, j);
}
// 基准元素和游标相遇时所指元素交换,为最后一次交换
exchange(a, low, j);
// 一趟排序完成, 返回基准元素位置
return j;
}
/**
* 交换两个数组元素
*/
private static void exchange(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}这里我们着重对 切分方法partition 做解读:
partition主要是以两部分组成: 外部while循环和两个并列的内部while循环。
两个内部while循环的作用是使得左右游标移动,最终相互靠近。
这里使用的【–】【++】运算符号,表明在进行循环表达式判断时,先进行-1、+1操作。
由于从左向右的指针是以头部开始的,所以这里while判断先+1,使得第一次判断位置在数列第二个数上(因为我们这里用第一个数为基准元素,所以不需要判断)。那么从右向左的指针为了平衡,也需要在while判断先-1,但这样最后一个数就无法在内了,这就是为什么上面 j 指针为什么初始化需要+1的原因。
外部While循环的作用是不断通过调用exchange方法使得指针停止下的元素相交换,从而让两指针 不断趋势靠近。
这里的
if (i >= j) {}表示两个指针最终相遇,跳出循环。
这里在第一个从右向左的循环的过程中,其实还可以再优化。里面的 if(j == low) break;这个判读是完全多余的,因为当j = low + 1的时候再执行判断时,j=pivotkey(因为–j,加上第一个数为基准元素),这时这一步判断根本不可能有执行的可能性的。
优化方法
优化-切换到插入排序:
快速排序在Java.Util的DualPivotQuicksort.clss类中定义了推荐使用长度为(47-286)之间:
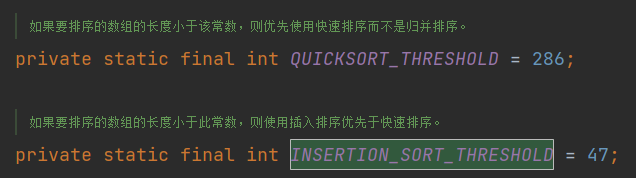
DualPivotQuicksort中定义了其排序数组长度在 小于 47时,使用插入排序方式排序,而长度大于286的时候。
这时或许有人会想到,在其外部排序的时候做判断 长度,来进行两种不同方式的排序。
然而这样对于快速排序没有本质上的优化,主要是在快速排序内部的数量优化。
所以这儿可以在其快速排序外部切分 递归时进行判断,如果递归下来的长度小于这个阈值就在该递归中执行快速排序即可。
只要把quickSort方法中的
if(high<= low) { return; }替换为:
if(high<= low + 47) { Insertion.sort(a,low, high) return; } // Insertion表示一个插入排序类优化-基准元素选取:
在上面的代码中我们的直接将其数列的首位元素作为了基准元素,这只是为了简单流程。
但是在大多数情况下,需要排序的数值或许不是随机生成的,而是存在一些顺序规则的,比如最糟糕的是 完全正序或完全逆序,我们如果始终还是以第一个为元素为基准元素的话,那么两个指针将会遍历所有步骤,快速排序的时间就会大大的加长,甚至沦为“慢速排序”。
为了解决这个问题,目前科学界上有三个优化方法:
- 排序前打乱数组的顺序
- 通过随机数保证取得的基准元素的随机性
- 三数取中法取得基准元素(推荐)
1、排序前打乱数组的顺序:
public static void sort (int [] a){
XXXRandom.shuffle(a) // 外部导入的乱序算法,打乱数组的分布
sort(a, 0, a.length - 1);
}当然这种执行一个乱序方法,这也会带来一部分耗时,这是需要注意的。
2、通过随机数保证取得的基准元素的随机性:
private static int getRandom (int []a, int low, int high) {
// 随机取出其中一个数组元素的下标
int RdIndex = (int) (low + Math.random()* (high - low));
// 将其和最左边的元素互换
exchange(a, RdIndex, low);
return a[low];
}
private static int partition (int[] a, int low, int high) {
int i = low, j = high+1;
// 基准元素随机化
int pivotkey = getRandom (a, low, high);
...
}这种方法通过随机取基准元素,来进行优化。它和第一个方法优势就是它不用随机全部数组元素,而是取随机长度即可。
3、三数取中法(推荐):
一般认为, 当取得的基准元素是数组元素的中位数的时候,排序效果是最好的,但是要筛选出待排序数组的中位数的不管是 时间成本还是资源成本都太高了, 所以只能从待排序数组中选取一部分元素出来再取中位数, 经大量实验显示: 当筛选的数组的长度为3时候,排序效果是比较好的, 所以由此发展出了三数取中法。
所谓三数取中法定义: 分别取出数组的最左端元素,最右端元素和中间元素, 在这三个数中取出中位数,作为基准元素。
// 选取左中右三个元素,求出中位数, 放入数组最左边的a[low]中
private static int selectMiddleOfThree(int[] a, int low, int high) {
int middle = low + (high - low)/2; // 取得位于数组中间的元素middle
if(a[low]>a[high]) {
exchange(a, low, high); //此时有 a[low] < a[high]
}
if(a[middle]>a[high]){
exchange(a, middle, high); //此时有 a[low], a[middle] < a[high]
}
if(a[middle]>a[low]) {
exchange(a, middle, low); //此时有a[middle]< a[low] < a[high]
}
return a[low]; // a[low]的值已经被换成三数中的中位数, 将其返回
}
private static int partition (int[] a, int low, int high) {
int i = low, j = high+1;
// 三数取中法 获取 基准元素
int pivotkey = selectMiddleOfThree (a, low, high);
...
}